摘要: Numpy基础学习笔记,记录了《利用python进行数据分析》学习过程和笔记。
Numpy(Numerical Python的简称)高性能科学计算和数据分析的基础包。其部分功能如下:
- ndarray,具有矢量算术运算和复杂广播能力的快速且节省空间的多维数组。
- 数组运算,不用编写循环
- 可以读写磁盘数据,操作内存映射
- 线性代数
- 集成c,c++等语言
python能够包装c、c++以numpy数组形式的数据。pandas提供了结构化或表格化数据的处理高级接口, 还提供了numpy不具备的时间序列处理等;
1.ndarray:多维数组对象
多维数组,要求所有元素的类型一致,通常说的“数组”、“Numpy数组”、“ndarray”都是指“ndarray”对象。
1.1 创建ndarray
| 函数 | 说明 |
|---|---|
| array | 输入数据转换为ndarray对象,可以是python元组、列表或其他序列类型。可以自动识别dtype,或者手动指定类型 |
| asarray | 将输入数据转换为ndarray对象 |
| arange | 类似range,返回ndarray的一维序列数组 |
| ones,ones_like | 创建全1数组,默认float类型。ones_like创建一个类型输入数组的全1数组 |
| zeros,zeros_like | 与ones相同,创建全0数组 |
| empty,empty_like | 全空数组,只分配内存空间,不填充任何值 |
| eye、identity | 创建一个n*n的单位矩阵(阵列) |
In [1]: import numpy as np
In [2]: np.arange(10)
Out[2]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [3]: np.array([1,2,3,5,6,7])
Out[3]: array([1, 2, 3, 5, 6, 7])
In [4]: np.ones((3,1))
Out[4]:
array([[ 1.],
[ 1.],
[ 1.]])
In [5]: np.zeros((2,5))
Out[5]:
array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
In [6]: np.eye(3)
Out[6]:
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
In [7]: np.empty((2,4))
Out[7]:
array([[ 0.00000000e+000, 0.00000000e+000, 2.12267575e-314,
2.19986168e-314],
[ 2.15551710e-314, 2.19976181e-314, 2.31584192e+077,
5.56268597e-309]])
1.2 ndarray数据类型
ndarry数组相关的数据类型
In [1]: import numpy as np
In [5]: a = np.array([1,2,4],dtype="int32")
In [6]: b = np.array([1,3,5],dtype=np.float32)
In [9]: a.dtype
Out[9]: dtype('int32')
In [10]: b.dtype
Out[10]: dtype('float32')
当需要控制数据在内存和磁盘中的存储方式时,尤其是大数据集,就需要了解如何控制存储类型。 dtype的表示形式有几种:
- 类型列中的值,使用字符串方式:如“int8”;
- 类型列中的值,使用如np.int8表示;
- 类型代码列中的值,使用字符串表示,如“f2”;
下表是所有支持的类型和说明:
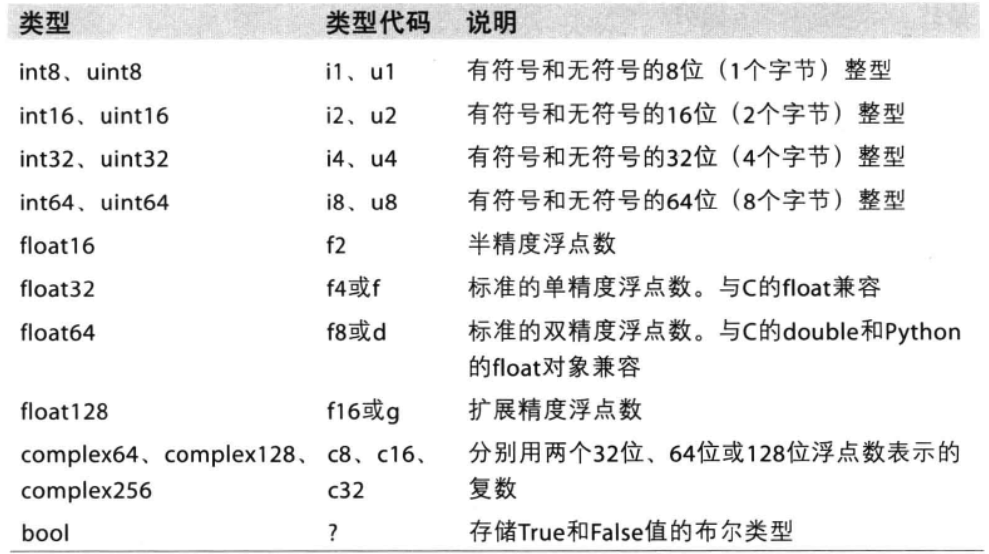

也可以使用astype修改dtype。
In [11]: a
Out[11]: array([1, 2, 4])
In [12]: c = a.astype("float64")
In [13]: c
Out[13]: array([ 1., 2., 4.])
In [14]: c.dtype
Out[14]: dtype('float64')
在格式转换过程中:
- 浮点数转换成整数,浮点数小数部分会被去掉;
- 如果字符串格式的数字,可以转换为数值形式;
- 复数转换
1.3 数组和标量之间的运算
数组的优势在于“矢量化”的运算,运算会应用到数组中的元素。 不需要编写循环进行运算,而且效率也比使用循环高。
In [17]: a
Out[17]:
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
In [18]: b
Out[18]:
array([[ 0, 2, 4, 6, 8],
[10, 12, 14, 16, 18]])
In [19]: a + b # 计算两个数组的和
Out[19]:
array([[ 0, 3, 6, 9, 12],
[15, 18, 21, 24, 27]])
In [21]: a * 10 # 每个元素*10
Out[21]:
array([[ 0, 10, 20, 30, 40],
[50, 60, 70, 80, 90]])
1.4 基本索引和切片
1.4.1 切片
Numpy切片功能与python的列用法是相同的,但是在是否复制切片数据是有区别的。
- python列表切片的时候复制数据
- Numpy数组切片直接操作原数组
python 列表切片操作
#
In [24]: list1 = list(range(10))
In [25]: list1
Out[25]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
In [26]: id(list1)
Out[26]: 104821896
In [27]: list1_slice = list1[2:5]
In [28]: id(list1_slice)
Out[28]: 104992840
In [29]: list1_slice
Out[29]: [2, 3, 4]
In [30]: list1_slice[0] = 100
In [31]: list1_slice
Out[31]: [100, 3, 4]
In [32]: list1 # 注意2号位置没有变化
Out[32]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Numpy 数组切片操作
In [33]: arr = np.arange(10)
In [34]: arr
Out[34]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [35]: id(arr)
Out[35]: 105028784
In [36]: arr_slice = arr[2:5]
In [37]: arr_slice
Out[37]: array([2, 3, 4])
In [38]: arr_slice[0] = 100
In [39]: arr_slice
Out[39]: array([100, 3, 4])
In [40]: id(arr_slice)
Out[40]: 105029024
In [41]: arr #2号位置被赋值了。
Out[41]: array([ 0, 1, 100, 3, 4, 5, 6, 7, 8, 9])
这样做的原因是Numpy为了能够更好的处理大数据集。如果每次复制将会大大的消耗内存。
1.4.2 索引
二维数组索引如下
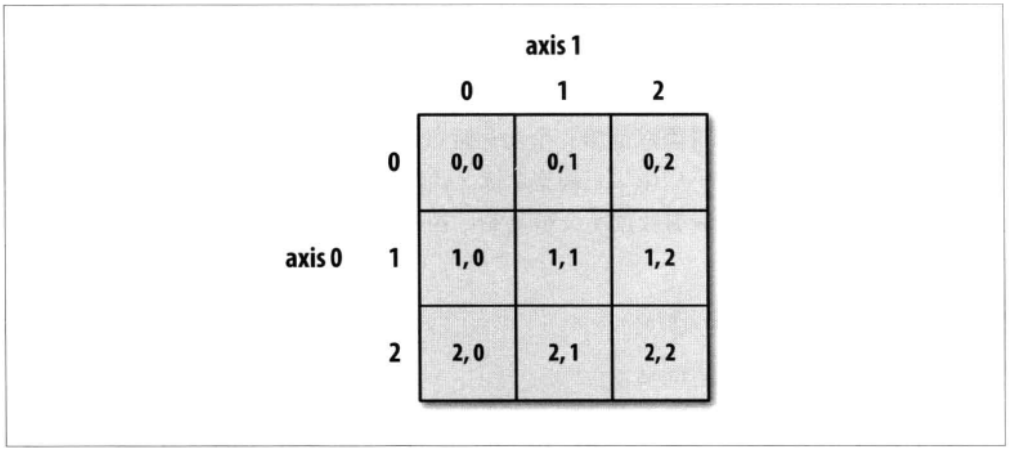
可以使用两种方式:
- 使用两个索引
- 使用两个值表示的列表作为索引
In [43]: a
Out[43]:
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
In [44]: a[0] #先行后列
Out[44]: array([0, 1, 2])
In [45]: a[0][1]
Out[45]: 1
In [46]: a[0,1]
Out[46]: 1
如果是多维数组的话,可以使用标量值或者数组来赋值。
In [50]: b
Out[50]:
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
In [51]: b[0]
Out[51]:
array([[1, 2, 3],
[4, 5, 6]])
In [52]: old_values = b[0]
In [53]: b[0] = 100
In [54]: b
Out[54]:
array([[[100, 100, 100],
[100, 100, 100]],
[[ 7, 8, 9],
[ 10, 11, 12]]])
In [55]: b[0] = old_values
In [56]: b
Out[56]:
array([[[100, 100, 100],
[100, 100, 100]],
[[ 7, 8, 9],
[ 10, 11, 12]]])
1.4.3 布尔型索引
直接看例子,有一组7*4的数据data,每行分别属于names数组中的人所有。
names = np.array(["Bob","Joe","Will","Bob","Will","Joe","Joe"])
data = np.random.randn(7,4)
names
Out[4]:
array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'],
dtype='<U4')
data
Out[5]:
array([[-0.3153179 , 1.01375816, -0.34210821, -0.74311504],
[-0.4196392 , -0.80468813, 0.65295259, 0.10492046],
[-0.40579151, 0.83195776, 0.71036512, -1.66161549],
[ 0.043161 , -0.68926623, -0.20530643, 0.82019059],
[-0.0088418 , -1.16661084, 0.36412278, -0.9806821 ],
[-0.02528605, -0.42485406, 0.26363666, -0.3005965 ],
[-1.62686502, 0.64529883, -0.23470384, 0.77666136]])
通过比较运算可以产生一个布尔型的数组,并把它作为索引
names == "Bob"
Out[6]: array([ True, False, False, True, False, False, False], dtype=bool)
data[names=="Bob"] #作为索引
Out[7]:
array([[-0.3153179 , 1.01375816, -0.34210821, -0.74311504],
[ 0.043161 , -0.68926623, -0.20530643, 0.82019059]])
data[names=="Bob",:2] #还能跟整数混用
Out[8]:
array([[-0.3153179 , 1.01375816],
[ 0.043161 , -0.68926623]])
还能这么用:
data[names!="Bob"]
Out[9]:
array([[-0.4196392 , -0.80468813, 0.65295259, 0.10492046],
[-0.40579151, 0.83195776, 0.71036512, -1.66161549],
[-0.0088418 , -1.16661084, 0.36412278, -0.9806821 ],
[-0.02528605, -0.42485406, 0.26363666, -0.3005965 ],
[-1.62686502, 0.64529883, -0.23470384, 0.77666136]])
data[-(names=="Bob")] # - 号已经不太使用,请使用~代替
Out[10]:
array([[-0.4196392 , -0.80468813, 0.65295259, 0.10492046],
[-0.40579151, 0.83195776, 0.71036512, -1.66161549],
[-0.0088418 , -1.16661084, 0.36412278, -0.9806821 ],
[-0.02528605, -0.42485406, 0.26363666, -0.3005965 ],
[-1.62686502, 0.64529883, -0.23470384, 0.77666136]])
data[~(names=="Bob")]
Out[11]:
array([[-0.4196392 , -0.80468813, 0.65295259, 0.10492046],
[-0.40579151, 0.83195776, 0.71036512, -1.66161549],
[-0.0088418 , -1.16661084, 0.36412278, -0.9806821 ],
[-0.02528605, -0.42485406, 0.26363666, -0.3005965 ],
[-1.62686502, 0.64529883, -0.23470384, 0.77666136]])
还有:
&表示和,|表示或- python中的and和or在ndarray中不能使用
mask = (names == "Bob")|(names =="Will" )
mask
Out[13]: array([ True, False, True, True, True, False, False], dtype=bool)
data[mask]
Out[14]:
array([[-0.3153179 , 1.01375816, -0.34210821, -0.74311504],
[-0.40579151, 0.83195776, 0.71036512, -1.66161549],
[ 0.043161 , -0.68926623, -0.20530643, 0.82019059],
[-0.0088418 , -1.16661084, 0.36412278, -0.9806821 ]])
同样,还能赋值
data[data < 0] =0
data
Out[16]:
array([[ 0. , 1.01375816, 0. , 0. ],
[ 0. , 0. , 0.65295259, 0.10492046],
[ 0. , 0.83195776, 0.71036512, 0. ],
[ 0.043161 , 0. , 0. , 0.82019059],
[ 0. , 0. , 0.36412278, 0. ],
[ 0. , 0. , 0.26363666, 0. ],
[ 0. , 0.64529883, 0. , 0.77666136]])
data[names=="Joe"] = 2
data
Out[20]:
array([[ 0. , 1.01375816, 0. , 0. ],
[ 2. , 2. , 2. , 2. ],
[ 0. , 0.83195776, 0.71036512, 0. ],
[ 0.043161 , 0. , 0. , 0.82019059],
[ 0. , 0. , 0.36412278, 0. ],
[ 2. , 2. , 2. , 2. ],
[ 2. , 2. , 2. , 2. ]])
1.4.4 花式索引
为了特定的选取行的子集,可以传入一个列表或者ndarray。
arr
Out[26]:
array([[ 0., 0., 0., 0.],
[ 1., 1., 1., 1.],
[ 2., 2., 2., 2.],
[ 3., 3., 3., 3.],
[ 4., 4., 4., 4.],
[ 5., 5., 5., 5.],
[ 6., 6., 6., 6.],
[ 7., 7., 7., 7.]])
arr[[4,2,1,5]]
Out[27]:
array([[ 4., 4., 4., 4.],
[ 2., 2., 2., 2.],
[ 1., 1., 1., 1.],
[ 5., 5., 5., 5.]])
arr_slice = [4,3,2,0]
arr[arr_slice]
Out[29]:
array([[ 4., 4., 4., 4.],
[ 3., 3., 3., 3.],
[ 2., 2., 2., 2.],
[ 0., 0., 0., 0.]])
也可以同时传入两个参数:
arr = np.arange(32).reshape(8,4)
arr
Out[31]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31]])
arr[[1,5,7,2],[0,3,1,2]]
Out[32]: array([ 4, 23, 29, 10])
# 两个列表的值分别对应一个索引值,形成4对索引。
花式索引与切片不一样,总是复制到新的数组中。
1.4.5 数组转置和轴对换
arr = np.arange(15).reshape(3,5)
arr
Out[34]:
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
arr.T
Out[35]:
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
# 来计算两个数组的内积
arr = np.random.randn(3,6)
np.dot(arr.T,arr)
Out[37]:
array([[ 3.72937613, -0.86744575, -1.62911498, -3.47666555, 0.32576022,
0.23910857],
[-0.86744575, 1.0711547 , 1.02242329, -1.08977196, -1.10673674,
0.33153465],
[-1.62911498, 1.02242329, 1.84009989, -0.32508586, -1.30894879,
-0.33134049],
[-3.47666555, -1.08977196, -0.32508586, 7.68163281, 2.21901489,
-0.72295841],
[ 0.32576022, -1.10673674, -1.30894879, 2.21901489, 1.50075102,
-0.12049286],
[ 0.23910857, 0.33153465, -0.33134049, -0.72295841, -0.12049286,
0.5919756 ]])
轴变换还没弄明白,待续。。。。
2.通用函数
快速的元素级数组函数
通用函数ufunc是一种对ndarray中的数据执行元素级运算的函数,可以理解为“简单函数的矢量化包装”。
现有的通用函数,如sqrt,exp等
a = np.arange(10)
np.sqrt(a) #求所有元素的平方根
Out[53]:
array([ 0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
np.exp(a) #求所有元素以e为底的幂
Out[54]:
array([ 1.00000000e+00, 2.71828183e+00, 7.38905610e+00,
2.00855369e+01, 5.45981500e+01, 1.48413159e+02,
4.03428793e+02, 1.09663316e+03, 2.98095799e+03,
8.10308393e+03])
2.1 一元通用函数
实例:
a = np.random.randn(4,4)
a
Out[65]:
array([[-1.35563407, 0.80045511, -0.750681 , -0.15750773],
[ 0.91350028, -0.73936677, -0.10522787, 1.95409707],
[-0.01240254, -3.28275315, 0.75904837, -0.78694871],
[ 2.13713841, -1.19244608, -0.11900042, -0.60834012]])
np.abs(a)
Out[68]:
array([[ 1.35563407, 0.80045511, 0.750681 , 0.15750773],
[ 0.91350028, 0.73936677, 0.10522787, 1.95409707],
[ 0.01240254, 3.28275315, 0.75904837, 0.78694871],
[ 2.13713841, 1.19244608, 0.11900042, 0.60834012]])
np.sqrt(a)
Out[69]:
array([[ nan, 0.89468157, nan, nan],
[ 0.95577208, nan, nan, 1.39789022],
[ nan, nan, 0.87123382, nan],
[ 1.46189549, nan, nan, nan]])
np.square(a)
Out[70]:
array([[ 1.83774372e+00, 6.40728378e-01, 5.63521970e-01,
2.48086851e-02],
[ 8.34482755e-01, 5.46663223e-01, 1.10729041e-02,
3.81849537e+00],
[ 1.53822884e-04, 1.07764683e+01, 5.76154422e-01,
6.19288270e-01],
[ 4.56736059e+00, 1.42192765e+00, 1.41610995e-02,
3.70077706e-01]])
np.exp(a)
Out[71]:
array([[ 0.25778379, 2.22655402, 0.47204498, 0.85427021],
[ 2.49303359, 0.47741613, 0.90011939, 7.0575437 ],
[ 0.98767406, 0.0375248 , 2.13624233, 0.45523172],
[ 8.47515051, 0.30347802, 0.88780743, 0.54425351]])
np.log10(a)
Out[72]:
array([[ nan, -0.09666302, nan, nan],
[-0.03929132, nan, nan, 0.29094613],
[ nan, nan, -0.11973055, nan],
[ 0.32983265, nan, nan, nan]])
np.sign(a)
Out[73]:
array([[-1., 1., -1., -1.],
[ 1., -1., -1., 1.],
[-1., -1., 1., -1.],
[ 1., -1., -1., -1.]])
np.ceil(a)
Out[74]:
array([[-1., 1., -0., -0.],
[ 1., -0., -0., 2.],
[-0., -3., 1., -0.],
[ 3., -1., -0., -0.]])
np.floor(a)
Out[75]:
array([[-2., 0., -1., -1.],
[ 0., -1., -1., 1.],
[-1., -4., 0., -1.],
[ 2., -2., -1., -1.]])
np.rint(a)
Out[76]:
array([[-1., 1., -1., -0.],
[ 1., -1., -0., 2.],
[-0., -3., 1., -1.],
[ 2., -1., -0., -1.]])
np.isnan(a)
Out[77]:
array([[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]], dtype=bool)
np.isfinite(a)
Out[78]:
array([[ True, True, True, True],
[ True, True, True, True],
[ True, True, True, True],
[ True, True, True, True]], dtype=bool)
np.cos(a)
Out[79]:
array([[ 0.21350595, 0.69638016, 0.7312245 , 0.98762128],
[ 0.61097851, 0.73889539, 0.99446865, -0.37398373],
[ 0.99992309, -0.99005339, 0.72549128, 0.70600953],
[-0.53654884, 0.3693879 , 0.9929278 , 0.82059778]])
np.arccos(a)
Out[80]:
array([[ nan, 0.64274221, 2.41988859, 1.7289627 ],
[ 0.41899009, 2.40292572, 1.67621936, nan],
[ 1.58319918, nan, 0.70894619, 2.47664439],
[ nan, nan, 1.69007941, 2.22476386]])
np.logical_not(a)
Out[81]:
array([[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]], dtype=bool)
2.2 二元通用函数
a = np.random.randint(0,100,(2,5))
a
Out[85]:
array([[44, 64, 35, 50, 79],
[68, 91, 62, 95, 8]])
b = np.random.randint(0,100,(2,5))
b
Out[87]:
array([[73, 17, 85, 19, 68],
[77, 62, 45, 49, 15]])
np.add(a,b)
Out[88]:
array([[117, 81, 120, 69, 147],
[145, 153, 107, 144, 23]])
np.subtract(a,b)
Out[89]:
array([[-29, 47, -50, 31, 11],
[ -9, 29, 17, 46, -7]])
np.multiply(a,b)
Out[90]:
array([[3212, 1088, 2975, 950, 5372],
[5236, 5642, 2790, 4655, 120]])
np.divide(a,b)
Out[91]:
array([[ 0.60273973, 3.76470588, 0.41176471, 2.63157895, 1.16176471],
[ 0.88311688, 1.46774194, 1.37777778, 1.93877551, 0.53333333]])
np.floor_divide(a,b)
Out[92]:
array([[0, 3, 0, 2, 1],
[0, 1, 1, 1, 0]], dtype=int32)
np.power(a,b) # 全超了最大值了
Out[93]:
array([[-2147483648, -2147483648, -2147483648, -2147483648, -2147483648],
[-2147483648, -2147483648, -2147483648, -2147483648, -2147483648]], dtype=int32)
np.maximum(a,b) #与max的区别
Out[94]:
array([[73, 64, 85, 50, 79],
[77, 91, 62, 95, 15]])
np.minimum(a,b)
Out[95]:
array([[44, 17, 35, 19, 68],
[68, 62, 45, 49, 8]])
np.mod(a,b)
Out[97]:
array([[44, 13, 35, 12, 11],
[68, 29, 17, 46, 8]], dtype=int32)
np.greater(a,b)
Out[98]:
array([[False, True, False, True, True],
[False, True, True, True, False]], dtype=bool)
a >b
Out[99]:
array([[False, True, False, True, True],
[False, True, True, True, False]], dtype=bool)
np.logical_and(a,b)
Out[100]:
array([[ True, True, True, True, True],
[ True, True, True, True, True]], dtype=bool)
2.3 自定义通用函数
待续。。。
3.数组处理数据
Numpy数组可以代替循环,进行矢量化的运算,通常会比纯python的方式快一两个数量级。
3.1 将条件逻辑表述为数组运算
np.where函数是x if condition else y的矢量化版本。
In [15]: yarr = np.array([2.1,2.2,2.3,2.4,2.5])
In [16]: cond = np.array([True,False,True,True,False])
In [17]: xarr = np.array([1.1,1.2,1.3,1.4,1.5])
In [18]: np.where(cond,xarr,yarr) # 判断cond条件,真zarr,假yarr
Out[18]: array([ 1.1, 2.2, 1.3, 1.4, 2.5])
另一个例子,希望将一组随机数,正数替换为2,负数替换为-2
In [19]: arr = np.random.randn(4,4)
In [20]: arr
Out[20]:
array([[ 1.18242592, 0.34138367, 0.36648288, 0.87214939],
[ 0.67129526, 0.2410077 , 0.37928273, -0.43982009],
[ 0.47559093, -0.050917 , -0.10229582, 1.58122926],
[ 0.83486166, -1.27310522, 0.17164926, 0.77951888]])
In [21]: np.where(arr > 0,2,-2)
Out[21]:
array([[ 2, 2, 2, 2],
[ 2, 2, 2, -2],
[ 2, -2, -2, 2],
[ 2, -2, 2, 2]])
In [22]: np.where(arr > 0,2,arr) # 负数还是arr
Out[22]:
array([[ 2. , 2. , 2. , 2. ],
[ 2. , 2. , 2. , -0.43982009],
[ 2. , -0.050917 , -0.10229582, 2. ],
[ 2. , -1.27310522, 2. , 2. ]])
3.2 数学和统计方法
这些方法一般可以作为实例方法调用,也可以当做Numpy函数使用。
In [23]: arr = np.random.randn(5,4)
In [24]: arr.mean()
Out[24]: -0.024836906150552153
In [25]: np.mean(arr)
Out[25]: -0.024836906150552153
基本数组统计方法如下:
In [26]: arr
Out[26]:
array([[-0.03065448, 0.91344557, -0.77812406, -1.608862 ],
[ 1.58463814, 0.98126805, 1.06389757, -1.17451329],
[ 1.48408281, 0.02386196, -0.80217916, 0.29413806],
[ 0.11536984, 1.73736452, 0.93596778, 0.26898712],
[-2.05527855, 0.49837502, -2.56571303, -1.38280997]])
In [27]: arr.sum()
Out[27]: -0.49673812301104303
In [28]: arr.sum(axis=0)
Out[28]: array([ 1.09815775, 4.15431511, -2.14615091, -3.60306008])
In [29]: arr.sum(axis=1)
Out[29]: array([-1.50419497, 2.45529046, 0.99990367, 3.05768925, -5.50542653]
)
In [30]: arr.mean()
Out[30]: -0.024836906150552153
In [31]: arr.mean(axis=1)
Out[31]: array([-0.37604874, 0.61382262, 0.24997592, 0.76442231, -1.37635663]
)
In [32]: arr.std()
Out[32]: 1.2223549632355621
In [33]: arr.var()
Out[33]: 1.4941516561466126
In [34]: arr.min()
Out[34]: -2.565713031578829
In [35]: arr.max()
Out[35]: 1.7373645152425918
In [36]: arr.argmin()
Out[36]: 18
In [37]: arr.cumsum()
Out[37]:
array([-0.03065448, 0.88279109, 0.10466703, -1.50419497, 0.08044316,
1.06171121, 2.12560878, 0.95109549, 2.4351783 , 2.45904026,
1.6568611 , 1.95099916, 2.066369 , 3.80373352, 4.73970129,
5.00868841, 2.95340986, 3.45178488, 0.88607184, -0.49673812])
In [38]: arr.cumprod()
Out[38]:
array([ -3.06544789e-02, -2.80011979e-02, 2.17884059e-02,
-3.50545383e-02, -5.55487582e-02, -5.45082216e-02,
-5.79911645e-02, 6.81113935e-02, 1.01082948e-01,
2.41203713e-03, -1.93488591e-03, -5.69123592e-04,
-6.56596961e-05, -1.14074826e-04, -1.06770361e-04,
-2.87198518e-05, 5.90272954e-05, 2.94177294e-05,
-7.54774516e-05, 1.04370972e-04])
3.3 用于布尔型数组的方法
布尔值是True和False,同时也是1和0。我们可以使用sum来统计True值得计数。
In [39]: arr
Out[39]:
array([[-0.03065448, 0.91344557, -0.77812406, -1.608862 ],
[ 1.58463814, 0.98126805, 1.06389757, -1.17451329],
[ 1.48408281, 0.02386196, -0.80217916, 0.29413806],
[ 0.11536984, 1.73736452, 0.93596778, 0.26898712],
[-2.05527855, 0.49837502, -2.56571303, -1.38280997]])
In [40]: (arr>0).sum()
Out[40]: 12
In [41]: arr>0
Out[41]:
array([[False, True, False, False],
[ True, True, True, False],
[ True, True, False, True],
[ True, True, True, True],
[False, True, False, False]], dtype=bool)
还有ang和all两个方法,可以用于布尔型数组,也可以用于非布尔型。在用于非布尔型数组时,所有非0元素都被当做True。
In [46]: bools = arr > 0 #将arr>0这个bool型数组赋值
In [47]: bools
Out[47]:
array([[False, True, False, False],
[ True, True, True, False],
[ True, True, False, True],
[ True, True, True, True],
[False, True, False, False]], dtype=bool)
In [48]: bools.any()
Out[48]: True
In [49]: bools.all()
Out[49]: False
In [50]: arr.any() #非0值将当成True处理。
Out[50]: True
3.4 排序
Numpy数组可以通过sort方法就地排序。
In [51]: arr
Out[51]:
array([[-0.03065448, 0.91344557, -0.77812406, -1.608862 ],
[ 1.58463814, 0.98126805, 1.06389757, -1.17451329],
[ 1.48408281, 0.02386196, -0.80217916, 0.29413806],
[ 0.11536984, 1.73736452, 0.93596778, 0.26898712],
[-2.05527855, 0.49837502, -2.56571303, -1.38280997]])
In [52]: arr.sort()
In [53]: arr
Out[53]:
array([[-1.608862 , -0.77812406, -0.03065448, 0.91344557],
[-1.17451329, 0.98126805, 1.06389757, 1.58463814],
[-0.80217916, 0.02386196, 0.29413806, 1.48408281],
[ 0.11536984, 0.26898712, 0.93596778, 1.73736452],
[-2.56571303, -2.05527855, -1.38280997, 0.49837502]])
In [54]: arr.sort(axis=0)
In [55]: arr
Out[55]:
array([[-2.56571303, -2.05527855, -1.38280997, 0.49837502],
[-1.608862 , -0.77812406, -0.03065448, 0.91344557],
[-1.17451329, 0.02386196, 0.29413806, 1.48408281],
[-0.80217916, 0.26898712, 0.93596778, 1.58463814],
[ 0.11536984, 0.98126805, 1.06389757, 1.73736452]])
In [56]: arr.sort(1)
In [57]: arr
Out[57]:
array([[-2.56571303, -2.05527855, -1.38280997, 0.49837502],
[-1.608862 , -0.77812406, -0.03065448, 0.91344557],
[-1.17451329, 0.02386196, 0.29413806, 1.48408281],
[-0.80217916, 0.26898712, 0.93596778, 1.58463814],
[ 0.11536984, 0.98126805, 1.06389757, 1.73736452]])
举个例子,求一个数组百分之5的分位数。
In [62]: arr = np.random.randn(1000)
In [63]: arr.sort()
In [64]: arr[int(0.05 * len(arr))]
Out[64]: -1.6307748333138019
In [67]: arr[50]
Out[67]: -1.6307748333138019
3.5 唯一化(去重)以及数组的集合运算
np.unique方法为数组去重,并排序。
In [68]: names = np.array(["Bob","Joe","Will","Bob","Will","Joe","Joe"])
In [69]: np.unique(names)
Out[69]:
array(['Bob', 'Joe', 'Will'],
dtype='<U4')
# 该方法类似于纯python中的如下:
In [70]: sorted(set(names))
Out[70]: ['Bob', 'Joe', 'Will']
其他集合运算:
In [71]: x = np.arange(1,101)
In [72]: y = np.arange(51,151)
In [73]: x
Out[73]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65,
66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78,
79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99, 100])
In [74]: y
Out[74]:
array([ 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76,
77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89,
90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102,
103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115,
116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128,
129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141,
142, 143, 144, 145, 146, 147, 148, 149, 150])
In [75]: np.intersect1d(x,y)
Out[75]:
array([ 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76,
77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89,
90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100])
In [77]: np.union1d(x,y)
Out[77]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65,
66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78,
79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104,
105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117,
118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130,
131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143,
144, 145, 146, 147, 148, 149, 150])
In [78]: np.in1d(x,y)
Out[78]:
array([False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True, True], dt
ype=bool)
In [79]: np.setdiff1d(x,y)
Out[79]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50])
In [80]: np.setxor1d(x,y)
Out[80]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 101, 102,
103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115,
116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128,
129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141,
142, 143, 144, 145, 146, 147, 148, 149, 150])
4.文件处理
Numpy可以读写文本数据或二进制数据。后续有pandas来处理文本,因此本部分简单介绍。
4.1 以二进制方式保存和读取numpy数组
单个数组,保存时会自动添加后缀名.npy
In [86]: arr = np.arange(10)
In [88]: np.save("some_array", arr)
In [90]: np.load("some_array.npy")
Out[90]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
多个数组,可以使用压缩方式存储,后缀名.npz
In [91]: arr
Out[91]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [92]: arr2 = np.arange(20)
In [93]: np.savez("array_archive.npz",a=arr,b=arr2)
In [94]: arch = np.load("array_archive.npz")
In [95]: arch
Out[95]: <numpy.lib.npyio.NpzFile at 0x7084f98>
In [96]: arch['b']
Out[96]:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19])
4.2 存取文本文件
使用np.savetxt和np.loadtxt两个方法来实现。后面会主要介绍pandas中的read_csv和read_table函数,这里不详细介绍。
In [99]: arr = np.random.randn(5,5)
In [102]: np.savetxt("arr.txt",arr,delimiter=",")
In [103]: np.loadtxt("arr.txt",delimiter=",")
Out[103]:
array([[ 0.45439906, -0.11067033, 1.67561654, 0.14142381, 0.1016269 ],
[-1.09070259, 0.41627682, -0.81896911, -0.14980666, -1.06391152],
[-0.88333647, 0.28268258, 0.69605952, 0.36348569, -0.53223699],
[-0.50561387, -0.65916355, 1.40181374, 1.17810701, 1.31155551],
[ 0.060254 , -1.02915195, -0.59382843, 0.49100178, -0.9541697 ]])
In [104]: arr
Out[104]:
array([[ 0.45439906, -0.11067033, 1.67561654, 0.14142381, 0.1016269 ],
[-1.09070259, 0.41627682, -0.81896911, -0.14980666, -1.06391152],
[-0.88333647, 0.28268258, 0.69605952, 0.36348569, -0.53223699],
[-0.50561387, -0.65916355, 1.40181374, 1.17810701, 1.31155551],
[ 0.060254 , -1.02915195, -0.59382843, 0.49100178, -0.9541697 ]])
5.线性代数
线性代数(Linear algebra)相关相关的有一个np.linalg可以解决这些问题。

import numpy as np
a = np.arange(1,10)
np.diag(a) # 以a的元素作为对角线值得方阵,其余值为0
Out[3]:
array([[1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 4, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 5, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 6, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 7, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 8, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 9]])
arr1 = np.array([[2,3,4],[2,5,3]])
arr2 = np.array([[2,4],[-3,4],[5,2]])
arr1.dot(arr2) #计算两个矩阵的内积
Out[6]:
array([[15, 28],
[ 4, 34]])
np.dot(arr1,arr2)
Out[8]:
array([[15, 28],
[ 4, 34]])
np.trace(np.diag(a)) #计算对角线之和
Out[9]: 45
arr3 = np.array([[1,2,3],[2,3,4],[5,4,2]])
np.linalg.det(arr3) # 求行列式
Out[12]: 0.99999999999999956
np.linalg.eig(arr3) # 求特征值和特征向量
Out[13]:
(array([ 8.75449624, -0.04211316, -2.71238309]),
array([[-0.41765986, -0.48871005, -0.42701284],
[-0.61198699, 0.79469434, -0.41357144],
[-0.67158928, -0.3600325 , 0.80412605]]))
arr4 = np.linalg.inv(arr3) #求逆矩阵m
arr4.dot(arr3) # 验证矩阵与逆矩阵的积
Out[17]:
array([[ 1.00000000e+00, -7.10542736e-15, -8.88178420e-15],
[ 3.55271368e-15, 1.00000000e+00, 2.66453526e-15],
[ 0.00000000e+00, -1.77635684e-15, 1.00000000e+00]])
np.linalg.solve(arr3,[2,5,4]) #求arr3和[2,5,4]的线性方程组的解
Out[19]: array([ 16., -25., 12.])
6.随机数
Numpy中有np.random作为python内置random模块的补充,增加了一些高效的函数。
Numpy的random模块不仅能生成1个样本值,也能产生大量样本值。
In [1]: import numpy as np #numpy库
In [2]: from random import normalvariate #python标准库
In [3]: %timeit samples = [normalvariate(0,1) for _ in range(1000000)]
1 loop, best of 3: 1.42 s per loop
In [4]: %timeit np.random.normal(size=1000000)
10 loops, best of 3: 39 ms per loop
可以看出,np.random要快很多。
部分例子:
In [6]: np.random.rand()
Out[6]: 0.7802183895038862
In [7]: np.random.rand(10)
Out[7]:
array([ 0.90918046, 0.90886419, 0.00794304, 0.64984129, 0.58132135,
0.9343964 , 0.19191809, 0.1478791 , 0.24818389, 0.36123808])
In [8]: np.random.randint(1,100)
Out[8]: 80
In [9]: np.random.randint(1,100,100)
Out[9]:
array([71, 47, 87, 16, 74, 96, 16, 82, 83, 6, 58, 60, 52, 79, 41, 14, 6,
28, 52, 7, 68, 61, 28, 26, 94, 42, 77, 26, 84, 61, 4, 71, 46, 72,
47, 8, 25, 43, 19, 63, 8, 69, 21, 56, 78, 98, 88, 60, 75, 41, 18,
21, 74, 25, 20, 71, 81, 91, 95, 12, 68, 15, 54, 75, 38, 51, 15, 79,
34, 34, 79, 28, 58, 56, 17, 44, 32, 58, 1, 16, 45, 74, 10, 15, 45,
14, 97, 36, 65, 61, 25, 55, 45, 78, 2, 99, 50, 14, 6, 6])
In [11]: np.random.randn(3,3)
Out[11]:
array([[ 0.31982232, -0.63358435, 0.05103954],
[-0.11613672, -0.8113278 , 0.29019726],
[-0.13409391, -0.81745446, 0.12032746]])
In [13]: np.random.binomial(0,1)
Out[13]: 0
In [16]: np.random.normal(10)
Out[16]: 9.555706096455244
seed()用于指定随机数生成时所用算法开始的整数值,如果使用相同的seed()值,则每次生成的随即数都相同,如果不设置这个值,则系统根据时间来自己选择这个值,此时每次生成的随机数因时间差异而不同。
In [17]: np.random.seed(0)
In [18]: np.random.randn(2,2)
Out[18]:
array([[ 1.76405235, 0.40015721],
[ 0.97873798, 2.2408932 ]])
In [19]: np.random.seed(0)
In [20]: np.random.randn(2,2)
Out[20]:
array([[ 1.76405235, 0.40015721],
[ 0.97873798, 2.2408932 ]])
# 两次生成的随机数居然相同
In [21]: np.random.randn(2,2)
Out[21]:
array([[ 1.86755799, -0.97727788],
[ 0.95008842, -0.15135721]])
# 第三次变了。
7.范例:随机漫步
随机漫步:从0开始,每次走一步,步长为1或者-1,概率相同。用python和numpy两种方式来实现。
7.1 用纯python实现
用纯python实现1000步的随机漫步。
import random
def random_walk_python(N):
postion = 0
walk = [postion]
for i in range(N):
step = 1 if random.randint(0,1) else -1
postion += step
walk.append(postion)
return walk
y = random_walk_python(1000)
#画个图看看,
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1001) #注意值个数
plt.plot(x,y)
plt.title("Random Walk")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
结果图:
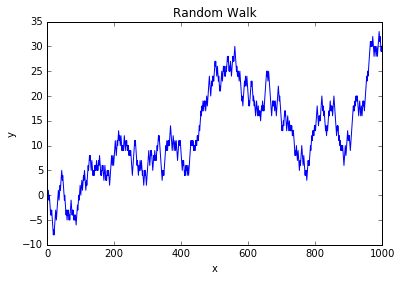
7.2 用numpy来实现
用numpy.random模块实现1000步随机漫步。
import numpy as np
def random_walk_numpy(N):
draws = np.random.randint(0,2,N) #创建0或1的1000个元素的随机一维数组
steps = np.where(draws > 0, 1,-1) #调整为1或-1的数组
walks = steps.cumsum() #计算累加和
return walks
yy = random_walk_numpy(1000)
#画图
import matplotlib.pyplot as plt
xx = np.arange(1000)
plt.plot(xx,yy)
plt.title("Random Walk")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
结果图:
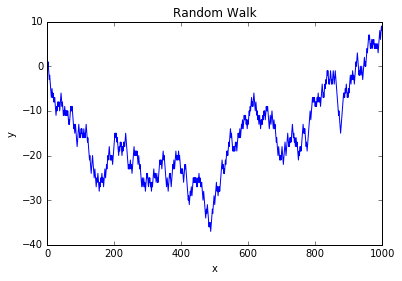
而且,我们很容易算出最大值,最小值。
yy.max() #最大值
Out[12]: 9
yy.min() #最小值
Out[13]: -37
yy.argmax() #最大值所在位置
Out[14]: 998
yy.argmin() #最小值所在位置
Out[15]: 488
7.2 同时实现多个随机漫步
比如一下子产生5000个随机漫步,每个随机漫步步数为1000。
In [22]: draws = np.random.randint(0,2,(5000,1000))
In [23]: steps = np.where(draws>0,1,-1)
# In [24]: walks = steps.cumsum()
In [32]: walks = steps.cumsum(axis= 1) # 按行累加
In [33]: walks
Out[33]:
array([[ -1, -2, -3, ..., 2, 1, 2],
[ 1, 2, 1, ..., 28, 27, 28],
[ 1, 0, 1, ..., 50, 49, 50],
...,
[ -1, -2, -3, ..., -36, -37, -38],
[ -1, -2, -3, ..., -2, -1, -2],
[ 1, 2, 1, ..., -40, -41, -40]], dtype=int32)
计算最大值和最小值
In [34]: walks.max()
Out[34]: 115
In [35]: walks.min()
Out[35]: -128
如果想要得到这五千个随机漫步达到30或-30的平均时间(步数),该如何计算?
In [37]: np.abs(walks)>= 30 #绝对值大于30的都为True
Out[37]:
array([[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False],
[False, False, False, ..., True, True, True],
...,
[False, False, False, ..., True, True, True],
[False, False, False, ..., False, False, False],
[False, False, False, ..., True, True, True]], dtype=bool)
In [38]: (np.abs(walks)>= 30).any(1) #选出有绝对值大于30的行
Out[38]: array([ True, True, True, ..., True, True, True], dtype=bool)
In [39]: hit30s = (np.abs(walks)>= 30).any(1)
In [40]: hit30s.sum() # 有3386行
Out[40]: 3386
In [41]: walks[hit30s] #选出这3386行
Out[41]:
array([[ -1, -2, -3, ..., 2, 1, 2],
[ 1, 2, 1, ..., 28, 27, 28],
[ 1, 0, 1, ..., 50, 49, 50],
...,
[ -1, -2, -3, ..., -36, -37, -38],
[ -1, -2, -3, ..., -2, -1, -2],
[ 1, 2, 1, ..., -40, -41, -40]], dtype=int32)
In [42]: np.abs(walks[hit30s])>=30
Out[42]:
array([[False, False, False, ..., False, False, False],
[False, False, False, ..., False, False, False],
[False, False, False, ..., True, True, True],
...,
[False, False, False, ..., True, True, True],
[False, False, False, ..., False, False, False],
[False, False, False, ..., True, True, True]], dtype=bool)
In [43]: (np.abs(walks[hit30s])>=30).shape
Out[43]: (3386, 1000)
#这些行中最大值所在位置,最大值就是1,也就是True,argmax会求出第一个最大值所在的位置。
In [44]: (np.abs(walks[hit30s])>=30).argmax(1)
Out[44]: array([701, 599, 667, ..., 103, 251, 671], dtype=int64)
In [46]: crossing_times = (np.abs(walks[hit30s])>=30).argmax(1)
In [47]: crossing_times.mean() #求这些最大值得平均值
Out[47]: 497.68340224453635







